Sai Aneesh Suryadevara

Reinforcement Learning (RL) is essentially learning from experiences. The basic premise of Reinforcement Learning is that we have an Agent, that performs actions in an Environment, and based on the feedback it receives, it learns over time, the correct action to take at every state.

RL seems very intuitive, right? Isn't this how we, as children learnt things? This direction of thinking may lead us to believe that RL might be the way to achieve AGI. However, with General Intelligence, the agent should be able to keep learning new tasks, without forgetting the skills it has learnt and also use it's existing knowledge as prior to learn new tasks. But the framework of RL leads to the agent making the best decisions on the current environment, and we get an agent specialised at a particular task.

Let us try to formulate the problem mathematically.

MDP

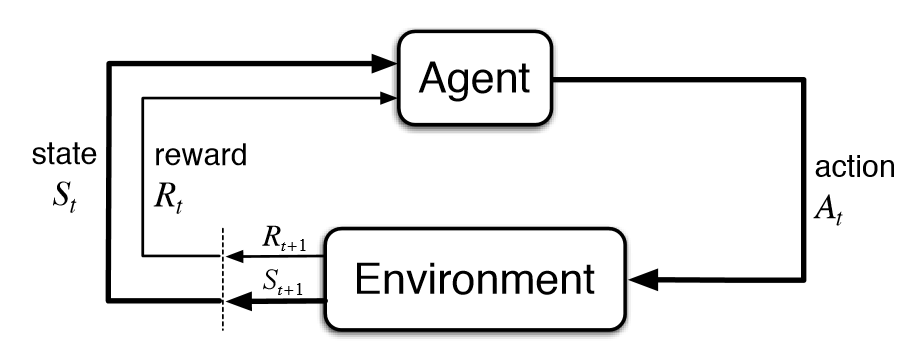
Assumption 1: Complete Observability
The agent gets to observe the complete state. Fully observable enviroment means that
Observation (\(O_t\)) = Agent State (\(S_t^a\)) = Environment State (\(S_t^e\)) = State (\(S_t\)).

History
Defined as the sequence of obervations, actions, rewards, \(H_t = A_1, O_1, R_1,...., A_t, O_t, R_t\)

State : History determines what happpens next. But it is not a helpful representation as it can become too large. State is essentially a concise summary that captures all the information we need to determine what happens next. For example, State can be the last 4 observations.

State Function
The state at any time is a function of its history: \(S_t = f(H_t)\)

Assumption 2: Markov Property
The next state \(S'\) depends solely on the current state \(S\). This is called the Markov Property. In simple terms it means “future outcomes depends solely on the present state- it doesn’t matter how we got to this state.”
\begin{equation} \mathbb{P}[S_{t+1} | S_t] = \mathbb{P}[S_{t+1} | S_1, S_2, …, S_t] \end{equation}

If considering the State as the Environment State \(S_t^e\), it is inherently Markov.
Viewing the State as the History \(H_t\) also conforms to Markov properties.

When we work with these two assumptions, we call it a Markov Decision Process

A Markov Decision Process is a tuple \(\langle \mathcal{S, A, P, R}, \gamma \rangle\)

\(\mathcal{S}\) is a finite set of states

\(\mathcal{A}\) is a finite set of actions

\(\mathcal{P}\) is a state transition probability matrix,
\begin{equation} \mathcal{P}(s’|s, a) = \mathbb{P}[S_{t+1} = s’ \mid S_t = s, A_t = a] \end{equation}

\(\mathcal{R}\) is a reward function, \(R\) is the reward \begin{equation} \mathcal{R}(s,a) = \mathbb{E}[R_{t+1} \mid S_t = s, A_t = a] \end{equation}

\(\gamma\) is a discount factor \(\gamma \in [0, 1]\)

There also exist partially observable markov decision processes (POMDPs) where the complete state of the system is not observable / the agent indirectly observes the environment. An example: The game of chess is an MDP, the state is completely observable, however, the a game of poker is a POMDP, where we do not know which cards the opponents have. In POMDPs, we don’t know the environment state. ( Agent State \(\neq\) Environment State). So in this case, the agent must construct its own representation of the state \(S_t^a\) e.g.,

Complete history: \(S_t^a = H_t\)
Beliefs of environment state: \(S_t^a = \left( P[S_t^e = s^1], \ldots, P[S_t^e = s^n] \right)\)

Policy, Value-Functions and The Bellman Equations

The return \(G_t\) is the total discounted reward from time-step \(t\).

\[G_t = R_{t+1} + \gamma R_{t+2} + \ldots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}\]

The value of receiving reward \(R\) after \(k + 1\) time-steps is \(\gamma^k R\).
\(\gamma \to 0\), implies we care about immediate reward and \(\gamma \to 1\), implies we care are far-sighted

A policy \(\pi\) is a distribution over actions given states,

\[\pi(a|s) = \mathbb{P}[A_t = a | S_t = s]\]

A policy fully defines the behaviour of an agent
MDP policies depend on the current state (not the history)
i.e., Policies are stationary (time-independent), \(A_t \sim \pi( . \mid S_t), \forall t > 0\)

The state-value function \(V_{\pi}(s)\) for an MDP is the expected return starting from state \(s\), and then following policy \(\pi\):

\[V_{\pi}(s) = \mathbb{E}_{\pi}[G_t \mid S_t = s]\]

Value of a State : From this state, if I take the best possible action at each subsequent step, what is the long-term reward I can expect?

The action-value function \(Q_{\pi}(s, a)\) is the expected return starting from state \(s\), taking action \(a\), and then following policy \(\pi\):

\[Q_{\pi}(s, a) = \mathbb{E}_{\pi}[G_t \mid S_t = s, A_t = a]\]

The state-value function can again be decomposed into immediate reward plus discounted value of successor state,

\[V_{\pi}(s) = \mathbb{E}_{\pi}[R_{t+1} + \gamma G_{t+1} \mid S_t = s]\]

Since, \(\mathbb{E}[X] = \mathbb{E}[\mathbb{E}[X \mid Y]]\) ( from Law of total expectation)

\[V_{\pi}(s) = \mathbb{E}_{\pi}[R_{t+1} + \gamma \mathbb{E}_{\pi}[G_{t+1} \mid S_{t+1} = s'] \mid S_t = s]\] \[V_{\pi}(s) = \mathbb{E}_{\pi}[R_{t+1} + \gamma V_{\pi}(S_{t+1}) \mid S_t = s]\] \[V_{\pi}(s) = \mathbb{E}_{\pi}[R_{t+1} \mid S_t = s] + \gamma \mathbb{E}_{\pi}[V_{\pi}(S_{t+1}) \mid S_t = s]\] \[V_{\pi}(s) = \sum_{r' \in R} r' \mathbb{P}(R_{t+1} = r' \mid S_t = s) + \gamma \sum_{s' \in \mathcal{S}}V_{\pi}(S_{t+1} = s') \mathbb{P}(S_{t+1} = s' | S_t = s)\] \[V_{\pi}(s) = \sum_{r' \in R} r' \sum_{a \in \mathcal{A}} \mathbb{P}(R_{t+1} = r', A_t= a | S_t=s) + \gamma \sum_{s' \in \mathcal{S}}V_{\pi}(S_{t+1} = s') \sum_{a \in \mathcal{A}}\mathbb{P}(S_{t+1} = s', A_t = a | S_t = s)\] \[V_{\pi}(s) = \sum_{a \in \mathcal{A}} \sum_{r' \in R} r' \mathbb{P}(R_{t+1} = r' | S_t=s, A_t= a)\mathbb{P}[A_t = a | S_t = s] + \gamma \sum_{s' \in \mathcal{S}}V_{\pi}(S_{t+1} = s') \sum_{a \in \mathcal{A}}\mathbb{P}(S_{t+1} = s', A_t = a | S_t = s)\] \[V_{\pi}(s) = \sum_{a \in \mathcal{A}} \mathbb{E}_{\pi}[R_{t+1} \mid S_t = s, A_t = a]\mathbb{P}[A_t = a | S_t = s] + \gamma \sum_{a \in \mathcal{A}}\mathbb{P}[A_t = a | S_t = s]\sum_{s' \in \mathcal{S}}\mathbb{P}(S_{t+1} = s' | S_t = s, A_t = a)V_{\pi}(S_{t+1} = s')\] \[V_{\pi}(s) = \sum_{a \in \mathcal{A}} \mathcal{R}(s,a)\pi(a|s) + \gamma \sum_{a \in \mathcal{A}}\pi(a|s) \sum_{s' \in \mathcal{S}}\mathcal{P}(s' | s,a)V_{\pi}(s')\]

The action-value function can similarly be decomposed,

\[Q_{\pi}(s, a) = \mathbb{E}_{\pi}[R_{t+1} + \gamma Q_{\pi}(S_{t+1}, A_{t+1}) \mid S_t = s, A_t = a]\]

Bellman Equations \begin{equation} V_{\pi}(s) = \sum_{a \in \mathcal{A}}\pi(a|s) \overset{Q_{\pi}(s,a)}{\left(\mathcal{R}(s,a) + \gamma \sum_{s’ \in \mathcal{S}}\mathcal{P}(s’ | s,a )V_{\pi}(s’)\right)} \end{equation} \begin{equation} Q_{\pi}(s,a) = \mathcal{R}(s,a) + \gamma\sum_{s’ \in S}\mathcal{P}(s’ |s,a) \sum_{a’ \in \mathcal{A}}\pi(a’|s’) Q_{\pi}(s’,a’) \end{equation}

The optimal state-value function \(V^* (s)\) is the maximum value function over all policies:

\[V^*(s) = \max_{\pi} V_{\pi}(s)\]

The optimal action-value function \(Q^*(s, a)\) is the maximum action-value function over all policies:

\[Q^*(s, a) = \max_{\pi} Q_{\pi}(s, a)\]

The Optimal Policy is given by: \(\pi^*(a|s) = \begin{cases} 1 & \text{if } a = \text{argmax}_{a \in A} Q^*(s, a) \\ 0 & \text{otherwise} \end{cases}\)

We can write,

\[V^*(s) = \max_a Q^*(s, a)\] \[Q^*(s,a) = \mathcal{R}(s,a) + \gamma\sum_{s' \in S}\mathcal{P}(s' \mid s,a) V^*(s')\]

The Bellman Optimality Equations are given by:
\[V^*(s) = \max_a \left( \mathcal{R}(s,a) + \gamma\sum_{s' \in S}\mathcal{P}(s' \mid s,a) V^*(s') \right)\] \[Q^* (s, a) = \mathcal{R}(s,a) + \gamma \sum_{s' \in S}\mathcal{P}(s'\mid s,a) \max_{a'} Q^* (s', a')\]

Value Iteration and Policy Iteration

Algorithm 1: Value Iteration

Inputs: Reward Function \(\mathcal{R}(s,a)\), state transition probabilties \(\mathcal{P}(s' \mid s,a)\)
Initialise \(V^{(0)}(s) = 0 \:\:\:\:\:\forall s \in S\)
While not converged, do:
- For \(s \in S\)
\[V^{(t+1)}(s) \leftarrow \max_{a \in \mathcal{A}} \left( \mathcal{R}(s,a) + \gamma\sum_{s' \in S} \mathcal{P}(s' \mid s,a) V^{(t)}(s') \right)\] \[t = t+1\]
Stopping: whenever \(V^{(t+1)}(s) = V^{(t)}(s)\), for all \(s\), we must have found \(V^*\)
Policy:

\[\pi^*(s) \leftarrow argmax_{a \in \mathcal{A}} \left( \mathcal{R}(s,a) + \gamma\sum_{s' \in S} \mathcal{P}(s' \mid s,a) V^{(t)}(s') \right)\]

Algorithm 2: Policy Iteration

Inputs: Reward Function \(\mathcal{R}(s,a)\), state transition probabilties \(\mathcal{P}(s' \mid s,a)\)
Initialise \(\pi\) randomly
While not converged, do:
- Solve the Bellman Equations defined by policy \(\pi\)
\[V^{\pi}(s) = \mathcal{R}(s,\pi(s)) + \gamma\sum_{s' \in S} \mathcal{P}(s' \mid s, \pi(s)) V^{\pi}(s')\]
- update \(\pi\)
\[\pi(s) \leftarrow argmax_{a \in \mathcal{A}} \left( \mathcal{R}(s,a) + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}(s' \mid s,a)V^{\pi}(s') \right)\]
Return \(\pi\)